Dalil Pythagoras merupakan salah satu dalil yang paling sering digunakan secara luas. Dalil ini pertama kali ditemukan oleh Pythagoras, yaitu seorang ahli matematika bangsa yunani yang hidup dalam abad keenam Masehi ( kira-kira pada tahun 525 sebelum Masehi ).
Dalil ini sesungguhnya telah dikenal orang-orang Babilonia sekitar 1.000 tahun sebelum masa kehidupan Pythagoras dan sampai saat ini masih digunakan antara lain untuk pelayaran, astronomi, dan arsitektur
Dalam segitiga siku-siku ABC, siku-siku di titik C, berlaku Dalil Pythagoras , yaitu :
c2 = a2 + b2
atau
Kuadrat sisi miring = jumlah kuadrat sisi-sisi yang saling tegak lurus
Pembuktian Dalil Pythagoras ada 3 cara, yaitu :
Cara Pertama:
Perhatikan Gambar dibawah ini :
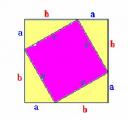
Pada gambar diatas, terdapat 4 segitiga siku-siku yang sebangun dan sama besar, persegi dengan panjang sisi c dan persegi dengan panjang sisi a + b. Luas Segitiga siku-siku tersebut masing-masing adalah 
, luas persegi yang didalam (warna pink) adalah c2 dan luas persegi yang besar (yang terluar) adalah (a + b)2 = a2 + 2ab + b2.
Dari gambar bidang tersebut, dapat kita peroleh persamaan yaitu :
Luas persegi yang terluar = luas persegi yang didalam + 4 luas segitiga siku-siku.
a2 + 2ab + b2 = c2 + 2 ab
a2 + 2ab + b2 – 2ab = c2
a2 + b2 = c2
Terbukti bahwa c2 = a2 + b2
Keterangan :
Luas persegi = sisi x sisi = s2
Luas segitiga = 
( a + b )2 = a2 + 2ab + b2
Cara 3 :
Perhatikan gambar di atas !
Luas persegi dengan panjang sisi a adalah 9 satuan luas ( 9 kotak ) atau a2
Luas persegi dengan panjang sisi b adalah 16 satuan luas ( 16 kotak ) atau b2
Luas persegi dengan panjang sisi c = luas persegi dengan panjang sisi a + luas persegi dengan panjang sisi b
| 25 satuan luas | = | 9 satuan luas | + | 16 satuan luas |
| 25 satuan luas | = | 25 satuan luas |
Kesimpulan :
c2 = a2 + b2
Keterangan :
Luas persegi = sisi x sisi = s2
Perhitungan panjang salah satu sisi segitiga siku-siku, Jika dua sisi yang lain diketahui
Dalam segitiga siku-siku ABC, siku-siku di titik C, berlaku :
| 1. | Jika sisi a dan b diketahui , maka sisi c dapat dihitung dengan rumus : c2 = a2 + b2 |
| 2. | Jika sisi b dan c diketahui , maka sisi a dapat dihitung dengan rumus : a2 = c2 - b2 |
| 3. | Jika sisi a dan c diketahui , maka sisi b dapat dihitung dengan rumus : b2 = c2 - a2 |
Tripel Pytagoras
Tiga buah bilangan a, b dan c dimana a, b dan ? bilagan asli dan c merupakan bilangan terbesar, dikatakan merupakan tripel Pythagoras jika ketiga bilangan tersebut memenuhi hubungan :
| c2 | = | a2+b2 | atau |
| b2 | = | c2-a2 | atau |
| a2 | = | c2-b2 |
CONTOH :
Manakah diantara tigaan berikut yang merupakan tripel Pythagoras ?
a. 9, 12, 15
b. 13, 14, 15
c. 5, 12, 13
PENYELESAIAN
| a. | Angka terbesar 15, maka c = 15, a = 12 dan b = 9 152 = 122 + 92 Jadi 9, 12, 15 merupakan tripel pythagoras |
| b. | Angka terbesar 15, maka c = 15, a = 13 dan b = 14 152 ¹ 132 + 142 |
| c. | Angka terbesar 13, maka c = 13, a = 12 dan b= 5132 = 122 + 52 169 = 144 +25 169 = 169 Jadi 5, 12, 13 merupakan tripel pythagoras |
Jenis Segitiga
Hubungan nilai c2 dengan ( a2 + b2 ) dapat digunakan untuk menentukan jenis segitiga. Jika a, b, dan c adalah panjang sisi-sisi suatu segitiga dengan :
c2 > a2 + b2
c2 = a2 + b2
c2 <>2 + b2
CONTOH :
Tentukanlah jenis segitiga berikut ( lancip, siku-siku, atau tumpul ), jika sisi-sisinya :
a. 6, 8, 10
b. 0,2 ; 0,3 ; 0,4
c. 11, 12, 14
No comments:
Post a Comment